Presentiamo alcuni teoremi che si applicano ai triangoli qualunque, che possono quindi essere utilizzati per triangoli rettangoli, isosceli, equilateri e scaleni.
Per i teoremi che illustreremo, consideriamo un triangolo ABC, di lati a, b, c.
Teorema dei seni
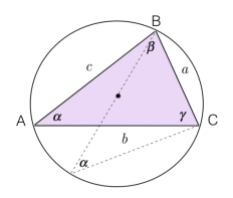
Le misure dei lati di un triangolo sono proporzionali ai seni degli angoli opposti.
In riferimento alla figura 1, abbiamo le seguenti relazioni:
\[ \color{red}{\boxed{\color{black}{\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma}}}} \]
Applicando questo teorema a un triangolo inscritto in una circonferenza, ci accorgiamo che esso deriva dall’applicazione del teorema della corda; in particolare, poiché ogni corda ( che corrisponde a un lato del triangolo ) è uguale al diametro per il seno di un angolo alla circonferenza corrispondente, possiamo scrivere che: \[ a = 2r \cdot \sin \alpha \rightarrow \frac{a}{\sin\alpha} = 2r \]
Quindi: \[ \frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma} = 2r \]
Possiamo quindi riformulare il teorema affermando che: in un triangolo rettangolo il rapporto di proporzionalità tra la misura di ciascun lato e il seno dell’angolo a esso opposto è uguale al diametro della circonferenza circoscritta al triangolo.
Teorema delle proiezioni
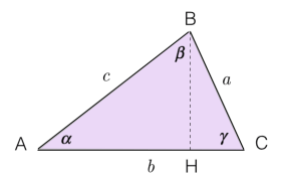
In un triangolo qualunque, la misura di un lato è uguale alla somma dei prodotti delle misure degli altri due lati per il coseno dell’angolo che ciascuno di questi forma con il primo.
In riferimento alla Figura 2, possiamo dare le seguenti relazioni:
\[ a = b \cdot \cos \gamma + c \cos \beta \] \[ b = a \cos \gamma + c \cos \alpha\] \[ c = \alpha \cdot \cos \beta + b \cos \alpha \]
Teorema del coseno o di Carnot
In un triangolo il quadrato della misura di un lato è uguale alla somma dei quadrati delle misure degli altri due, diminuito del doppio prodotto delle misure di questi due lati per il coseno dell’angolo tra essi compreso.
Quindi, abbiamo le seguenti relazioni:
\[ a^2 = b^2 + c^2 – 2bc\cdot \cos \alpha \]
\[ b^2 = a^2 + c^2 – 2ac\cdot \cos \beta \]
\[ c^2 = a^2 + b^2 – 2ab\cdot \cos \gamma \]
In questo modo, possiamo determinare un lato di un triangolo conoscendo gli altri due, e l’angolo tra essi compreso.
Possiamo sfruttare questo teorema anche per determinare l’angolo compreso tra due lati, conoscendo tutti e tre i lati del triangolo; in questo caso, si ha:
\[ \cos\alpha=\frac{b^2+c^2-a^2}{2bc} \,\,\, ,\,\,\, \cos\beta=\frac{a^2+c^2-b^2}{2ac}\,\,\, , \,\,\, \cos\gamma=\frac{a^2+b^2-c^2}{2ab} \]
Notiamo che, nel caso in cui l’angolo compreso tra i due lati sia un angolo retto, misuri, cioè, \(\pi/2\), il teorema di Carnot si riduce al teorema di Pitagora, in quanto il coseno di un angolo retto è zero:
\[ a^2 = b^2 + c^2 – 2bc \cdot \cos\alpha = b^2 + c^2 – 2b \cos \frac{\pi}{2} = b^2 + c^2 \]
Risoluzione di un triangolo qualunque
Esaminiamo, ora, alcuni casi che si possono presentare, e vediamo come agire per determinare tutti i dati relativi ad un triangolo qualunque.
Caso 1: Consideriamo un triangolo ABC, con lati a, b, c, di cui sono noti un lato e due angoli, ad esempio il lato a, e gli angoli \(\beta\) e \(\gamma\).
Possiamo determinare il terzo angolo ricordando che la somma degli angoli interni di un triangolo è di 180°; poi, possiamo applicare il teorema dei seni per determinare gli altri due lati del triangolo: \[ \alpha = 180^{\circ} – \beta – \gamma \] \[ \frac{a}{\sin\alpha} = \frac{b}{\sin\beta} \,\,\,\ \text{ e } \,\,\, \frac{a}{\sin\alpha} = \frac{c}{\sin\gamma} \]
Caso 2: Consideriamo un triangolo ABC, con lati a, b, c, di cui sono noti due lati e l’angolo tra essi compreso, ad esempio i lati a e b, e l’angolo γ.
In questo caso, possiamo applicare il teorema del seno per determinare il terzo lato, poi, conoscendo le misure dei tre lati, possiamo utilizzare lo stesso teorema per determinare le funzioni goniometriche degli angoli restanti.
Caso 3: Consideriamo un triangolo ABC, con lati a, b, c, di cui sono noti tutti e tre i lati; dobbiamo, quindi, calcolare tutti gli angoli del triangolo.
In questo caso, il teorema di Carnot ci fornisce il metodo più semplice ed immediato per risolvere il triangolo; applicando la formula inversa del teorema, infatti, possiamo calcolare il coseno di tutti gli angoli del triangolo: \[ \cos\alpha = \frac{c^2+b^2-a^2}{2cb} \] \[ \cos\beta = \frac{c^2+a^2-b^2}{2ac}\] \[ \cos\gamma = \frac{a^2+b^2-c^2}{2ab} \]
L'articolo Risoluzione triangoli qualunque sembra essere il primo su Matematicamente.