L’equazione di Bernoulli e l’effetto Venturi

L’equazione di Bernoulli

Quando un fluido si muove all’interno di una conduttura, può capitare che essa non sia regolare; ad esempio, esso può presentare restringimenti e allargamenti; oppure può essere per alcuni tratti orizzontale e per altri in discesa, può presentare delle curvature, ecc.

Tutti questi aspetti fanno si che studiare il moto del fluido risulti molto complicato; infatti, vi sono molte grandezze relative al fluido che si possono modificare in maniera repentina e difficile da prevedere.

Tra queste possono essere modificate la velocità del fluido, la pressione che esso esercita sulle pareti della conduttura, la quota a cui si trova.

Quando si studiano i fluidi, quindi, molto spesso si assume che il fluido in questione sia incompressibile, che la corrente sia stazionaria (cioè che la portata del fluido sia costante nel tempo) e si trascurano gli attriti del fluido con le pareti della conduttura e gli attriti interni.

Sotto queste ipotesi, Bernoulli formulò una legge che permette di relazionare la velocità, la pressione e la quota cui si trova un fluido:

$ p + 1/2dv^2 + dgy = cost$

Nella formula indichiamo con d la densità del fluido, con y la sua quota; g è l’accelerazione di gravità e vale $9,81 m/s^2$.

La formula prende il nome di equazione di Bernoulli.

L’equazione, quindi, afferma che in due posizioni diverse all’interno di una conduttura (che indichiamo con A e B), che differiscono per valori di velocità, pressione e quota del fluido, rimane in ogni caso costante quella particolare relazione che vi è tra le grandezze.

Abbiamo, quindi, la seguente uguaglianza:

$ p_A + 1/2dv_A^2 + dgy_A = p_B + 1/2dv_B^2 + dgy_B $

L’effetto Venturi

Esaminiamo il caso particolare in cui la conduttura sia orizzontale; per tutto il suo percorso, quindi, il fluido si troverà sempre alla stessa quota, e avremo quindi che $y_A$ = $y_B$ per ogni posizione.

La legge di Bernoulli, quindi, assume la seguente forma:

$ p_A + 1/2dv_A^2 = p_B + 1/2dv_B^2 $

Poiché la densità del liquido rimane la stessa, l’equazione mostra che se la pressione nel primo tratto (A) è maggiore di quella nel secondo tratto (B), necessariamente la velocità del fluido in A deve essere minore di quella in B.

Questo particolare effetto è noto come effetto Venturi.

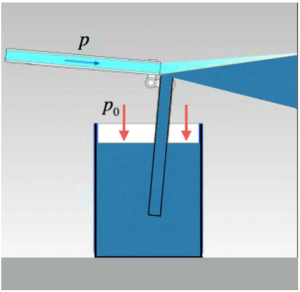
Un esempio di applicazione dell’effetto Venturi è quello del nebulizzatore a bocca.

In questo caso l’aria che viene soffiata dalla bocca all’interno della cannuccia si comporta come un fluido incompressibile, e con il suo flusso aspira il fluido contenuto nel serbatoio; questo risale lungo il tubicino e viene poi nebulizzato all’estremità di esso.

Ciò accade perché dove il tubo si restringe la velocità dell’aria aumenta (equazione di continuità); dall’equazione di Bernoulli sappiamo che in tale zona la pressione dell’aria (p) è minore di quella atmosferica (p0) che agisce sulla superficie della vernice nel serbatoio. Per questo, la vernice viene aspirata verso l’alto e sprizzata fuori dal getto d’aria che incontra all’estremità del tubicino.

nebulizzatore-a-bocca — Esperimento del nebulizzatore a bocca.

Esercizio

Consideriamo una conduttura orizzontale all’interno della quale scorre dell’olio d’oliva, con densità $d = 920 kg/m^3$. La conduttura presenta due tratti diversi: nel primo tratto, quello più stretto, l’olio scorre con una velocità di 4,0 m/s, ed esercita una pressione di $5,1 * 10^4 Pa$. Nel secondo tratto, invece, la velocità dell’olio è di 2,0 m/s. Calcolare la pressione esercitata dall’olio nel secondo tratto.

Il problema può essere risolto con la legge derivante dall’effetto Venturi, in quanto la conduttura che stiamo considerando si trova in orizzontale, e quindi la quota del liquido in due tratti differenti è sempre la stessa. Indichiamo, quindi, con 1 il primo tratto e con 2 il secondo; abbiamo la seguente relazione:

$ p_1 + 1/2dv_1^2 = p_2 + 1/2dv_2^2 $

Dalla relazione precedente, possiamo ricavare il valore della pressione nel secondo tratto:

$p_2 = p_1 + 1/2dv_1^2 – 1/2dv_2^2$

Sostituiamo i valori numerici e determiniamo il valore della pressione nel secondo tratto:

$p_2 = 5,1 * 10^4 + 1/2*920*4^2 – 1/2 *920*4^2 = 56520 Pa = 5,7 * 10^4 Pa$

In accordo con l’effetto Venturi, troviamo che la pressione nel secondo tratto, in cui il fluido si muove con velocità minore, è maggiore di quella nel primo tratto, deve invece la velocità dell’olio è maggiore.