Definizione: Dato un punto O del piano, e un numero reale γ, si definisce rotazione di centro O e angolo γ, e si scrive:
\[ \rho_{O,\gamma} \]
la corrispondenza biunivoca tra i punti del piano che associa al punto O il punto O stesso, e che ad ogni punto P diverso da O associa il punto P’ tale che:
\[ \widehat{POP’} = \gamma(\mbox{mod}\, 2\pi) \,\,\,\, , \,\,\,\, \overline{OP} = \overline{OP’} \]
In particolare, il punto P’ appartiene alla circonferenza di centro O e raggio OP; distinguiamo alcuni casi, in base al tipo di angolo che descrive la rotazione: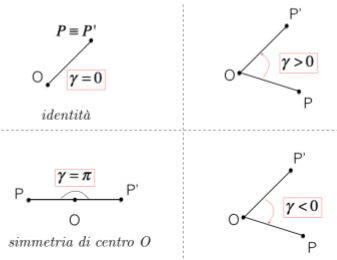
- Se \( \gamma = 0 \), la rotazione è l’identità;
- Se \( \gamma = \pi \), la rotazione è una simmetria di centro O;
- Se \(\gamma\) è positivo, la rotazione è il senso orario, mentre se \(\gamma\) è negativo, la rotazione è in senso antiorario.
Possiamo quindi notare che, nel caso in cui l’angolo di rotazione sia diverso da zero, il solo punto che viene mandato in se stesso è il punto O, quindi, il punto O è il solo punto unito.
Possiamo affermare, poi, che è unita ogni circonferenza di centro O.
La rotazione è un’isometria.
Consideriamo i punti del piano P e Q, e applichiamo su di essi una rotazione di centro O e angolo \(\gamma\), tale che al punto P corrisponda il punto P’, e al punto Q corrisponda il punto Q’.
Poiché i triangoli che si formano, OPQ e OP’Q’ sono congruenti, possiamo affermare che anche i loro lati corrispondenti sono congruenti, e in particolare si ha che PQ = P’Q’; quindi, poiché la trasformazione preserva le distanze, essa è un’isometria.
Formule analitiche
Anche nel caso delle rotazioni, esistono delle formule che ci permettono di determinare le coordinate di un nuovo punto P’, ottenuto applicando una rotazione di un angolo noto \(\gamma\) (del quale dobbiamo poter determinare le funzioni goniometriche) ad un punto iniziale P, del quale conosciamo le coordinate.
Se il punto P in questione ha coordinate (x; y), e il punto P’ ha coordinate (x’; y’), la rotazione di centro l’origine è descritta dalle seguenti equazioni:
\[ \rho_{O,\gamma}=\begin{cases} x’=x\cdot \cos\gamma-y\cdot\sin\gamma \\ y’=x\cdot\sin\gamma+y\cdot\cos\gamma \end{cases} \]
La matrice A dei coefficienti delle equazioni, in questo caso, è la seguente:
\[ A = \begin{pmatrix} \cos\gamma & -\sin\gamma \\ \sin\gamma & \cos\gamma \end{pmatrix} \]
e il suo determinante è sempre uguale ad 1, infatti risulta che:
\[ \mbox{det}(A) = \cos\gamma \cdot\cos\gamma – (-\sin\gamma \cdot\sin\gamma =\cos^2\gamma +\sin^2\gamma = 1\]
Da questa osservazione possiamo dedurre che tutte le affinità che hanno equazioni:
\[ \begin{cases} x’=ax-by \\ y’=bx+ay \end{cases} \]
e tali che il determinante della matrice dei coefficienti sia uguale ad 1, cioè, tali che
\[ a^2 + b^2 = 1 \]
sono rotazioni di centro l’ordine e angolo γ tale che \(\cos(γ) = a\) e \( \sin(γ) = b\).
E’ possibile determinare anche la trasformazione inversa di una rotazione di angolo γ, che corrisponde ad una rotazione di uguale centro, ma di angolo -γ; essa è descritta dalle seguenti equazioni:
\[ \rho^{-1}_{O,\gamma} = \rho_{O,-\gamma} = \begin{cases} x=x’\cos\gamma + y’\cdot \sin\gamma \\ y=-x’\cdot \sin\gamma + y’\cdot \cos\gamma \end{cases} \]
Esempio: Consideriamo i punti P di coordinate (1; 0) e Q di coordinate (0; 1), e la retta r passante per P e Q. Vogliamo determinare la retta r’, trasformata di r mediante la rotazione di angolo \(\gamma = \pi/3\).
Conoscendo le coordinate dei punti P e Q, possiamo ricavare l’equazione della retta r che passa per essi:
\[ r: \frac{y-0}{1-0} = \frac{x-1}{0-1} \rightarrow r:x+y-1=0 \]
L’angolo di rotazione è un angolo noto, di cui conosciamo le funzioni goniometriche; quindi, possiamo scrivere le formule generali della rotazione di angolo \(\pi/3\):
\[\rho_{O,\frac{\pi}{3}} = \begin{cases} x’=\frac{1}{2}x-\frac{\sqrt{3}}{2}y \\ y’=\frac{\sqrt{3}}{2}x-\frac{1}{2}y\end{cases} \]
Avendo determinato la formula generale della rotazione, per individuare le nuove coordinate dei punti non dobbiamo far altro che sostituire le coordinate di P e Q nelle equazioni:
\[ P’: \begin{cases} x’=\frac{1}{2}\cdot 1-\frac{\sqrt{3}}{2}\cdot 0 \\ y’=\frac{\sqrt{3}}{2} \cdot 1 + \frac{1}{2}\cdot 0 \end{cases} \,\,\,\,,\,\,\,\, Q’: \begin{cases} x’=\frac{1}{2}\cdot 0-\frac{\sqrt{3}}{2}\cdot 1 \\ y’=\frac{\sqrt{3}}{2} \cdot 0 + \frac{1}{2}\cdot 1 \end{cases} \]
Da cui otteniamo che:
\[ P’: \Big(\frac{1}{2}; \frac{\sqrt{3}}{2} \Big)\,\,\,\, , \,\,\,\, Q’: \Big(-\frac{\sqrt{3}}{2}; \frac{1}{2}\Big) \]
Avendo determinato le coordinate dei nuovi punti, possiamo ricavare l’equazione della rette r’, passante per P’ e Q’:
\[ r’: \frac{y’-\frac{\sqrt{3}}{2}}{\frac{1}{2}-\frac{\sqrt{3}}{2}} = \frac{x’+\frac{\sqrt{3}}{2}}{\frac{1}{2}+\frac{\sqrt{3}}{2}} \rightarrow r’:(\sqrt{3}-1)x’-(\sqrt{3}+1)y’+2=0 \]
Rappresentiamo le rette graficamente:

Potrebbero interessarti
- Affinità e trasformazioni
- Isometrie e traslazioni
- La simmetria centrale
- La simmetria assiale
- Similitudine e omotetia
- Dilatazioni e compressioni, inclinazioni
- Inversione rispetto al cerchio
- Cambiamenti di riferimento nel piano
- Le coordinate polari nel piano
- Grafici in coordinate polari
- Trasformazioni lineari e matrici
L'articolo Rotazioni sembra essere il primo su Matematicamente.