Come abbiamo visto nel caso delle onde sonore, se la sorgente che emette il suono e il rilevatore che lo riceve sono in moto relativo tra loro, la frequenza o la lunghezza d’onda del segnale che viene percepito dall’osservatore varia. In questo modo, l’osservatore può capire se la sorgente si sta allontanando o avvicinando in base al suono che percepisce.
Ricordiamo che vi sono delle relazioni tra le frequenze percepite e quelle emesse; in generale, se la sorgente e l’osservatore si muovono sulla stessa retta e si stanno avvicinando, la frequenza che l’osservatore percepisce è data dalla formula:
$v’ = v * frac(1 + frac(V_R)(V_o))(1 – frac(V_S)(V_o))$
dove v è la frequenza emessa dall’onda, mentre $Vr$, $V_s$ e $V_o$ sono, rispettivamente, le velocità del rilevatore, della sorgente e dell’onda.
Nel caso in cui il rilevatore e la sorgente si stiano allontanando, invece, la formula è la seguente:
$v’ = v * frac(1 – frac(V_R)(V_o))(1 + frac(V_S)(V_o))$
L’effetto doppler e le onde luminose
L’effetto doppler si manifesta anche nel caso di onde luminose; in astronomia, ad esempio, questo fenomeno è studiato per capire se le galassie sono in allontanamento o in avvicinamento.
Nel caso di onde luminose, però, le formule che permettono di determinare le nuove frequenze percepite dal rilevatore sono diverse. Per prima cosa, mentre per le onde sonore la velocità di propagazione dell’onda dipende dalla velocità della sorgente, nel caso della luce, non potendo applicare la legge di composizione delle velocità, da velocità dell’onda è sempre la stessa, indipendentemente dal fatto che la sorgente sia ferma o in moto.
Inoltre, poiché la luce si propaga nel vuoto, e non in un mezzo, non è possibile capire se a muoversi sia la sorgente o l’osservatore, e quindi si parla di velocità relativa osservatore-sorgente.
Si può dimostrare che la frequenza v’ del segnale che viene percepita dall’osservatore nel caso in cui osservatore e sorgente si allontanano è data dalla seguente formula:
$ v’ = v * frac(sqrt(1 – frac(V_r)(c)))(sqrt(1 + frac(V_r)(c))) = frac(sqrt(1 – β))(sqrt(1 + β))$
con Vr = velocità relativa osservatore-sorgente. In questo caso, quindi, la frequenza rilevata è minore di quella emessa.
Nel caso in cui, invece, l’osservatore e la sorgente siano in avvicinamento, la formula vale con i segni invertiti:
$ v’ = v * frac(sqrt(1 + frac(V_r)(c)))(sqrt(1 – frac(V_r)(c))) = frac(sqrt(1 + β))(sqrt(1 – β))$
In questo caso, invece, la frequenza rilevata è maggiore di quella emessa.
L’effetto doppler e le galassie
Come accennato precedentemente, lo studio dell’effetto doppler nel caso di onde luminose è particolarmente utilizzato in astrofisica, in quanto esso rappresenta uno dei pochi modi che si hanno per studiare le galassie, e per capire se esse sono in avvicinamento o in allontanamento rispetto alla Via Lattea, e determinare la velocità a cui si spostano.
Questo studio si basa sul fatto che lo spettro emesso dalle stelle è uno spettro a righe di assorbimento; l’effetto doppler si manifesta quando, esaminando lo spettro emesso da una stella, si notano righe di assorbimento che si trovano in posizioni diverse rispetto rispetto allo stesso spettro misurato in laboratorio.
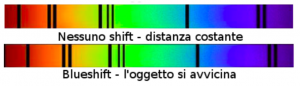
Si deduce, quindi, che vi è una variazione della lunghezza d’onda, e quindi della frequenza che vengono percepite; in particolare, poiché lo spettro del visibile presenta come colori marginali il blu e il rosso, si parla di “spostamento verso il rosso”, o redshift se lo spettro presenta righe spostate verso lunghezze d’onda maggiori:

altrimenti si parla di “spostamento verso il blu”, o blueshift nel caso di spostamento verso lunghezze d’onda minori.
Si definisce, quindi, il numero puro z, dato da:
$ z = frac(v)(v’) – 1 $
Tale numero permette di capire, a partire dalle frequenze emessa e percepita, se la sorgente si sta avvicinando o allontanando dall’osservatore: in caso di redshift si hanno valori positivi di z, mentre in caso di blueshift si hanno valori negativi.
Nel caso in cui z = 0, la frequenza percepita è uguale alla frequenza emessa, e quindi l’osservatore e la sorgente sono in quiete.
Potrebbero Interessarti
Video Lezioni: Relatività
Appunti: La velocità della luce
Appunti: L’esperimento di Michelson-Morley
Appunti: La relatività ristretta
Appunti: La dilatazione del tempo
Appunti: La contrazione delle lunghezze
Appunti: Le trasformazioni di Lorentz
Appunti: L’intervallo invariante
Appunti: Lo spazio-tempo di Minkowski
Appunti: Equivalenza massa-energia
Appunti: La relatività generale
Appunti: La curvatura dello spazio-tempo
Appunti: La deflessione gravitazionale della luce
L'articolo L’effetto doppler relativistico sembra essere il primo su Matematicamente.