Il campo elettrico

Una spiegazione alternativa per l’attrazione tra corpi carichi

Come abbiamo visto in precedenza, esiste una forza, detta forza di Coulomb, responsabile dell’attrazione tra cariche elettriche di segni opposti; tale forza è una forza a distanza, come la forza di attrazione gravitazionale.

In un primo momento, quindi, si pensava l’interazione tra corpi carichi solo come effetto della forza di Coulomb.

Intorno alla metà dell’ottocento, però, fu introdotto un nuovo punto di vista sul fenomeno, ad opera dello scienziato inglese Michael Faraday. Egli spiegò il fenomeno dell’interazione tra corpi carichi con il concetto di campo elettrostatico.

Egli affermò che anche una singola carica elettrica è in grado di generare un campo elettrico, indipendentemente dal fatto che sia presente o meno una seconda carica con cui essa interagisca.

Anche in questa nuova interpretazione, pero, la forza di Coulomb continua ad agire.

Consideriamo una carica $Q_1$ ; la sua presenza nello spazio modifica lo spazio circostante, cosicché le proprietà di ogni punto di esso vengono modificate.

Se in tale spazio è presente una carica $Q_2$ , essa risente ella modifica dello spazio in cui si trova avvertendo una forza elettrica, quella di Coulomb.

Campo elettrico e telo elastico

Per capire meglio il concetto di campo elettrico, ipotizziamo che lo spazio possa essere rappresentato con un telo elastico, e la carica con una sfera.

Supponiamo che una carica Q si trovi nello spazio; nel nostro modello, se poniamo una sfera sopra un telo elastico, notiamo che esso si piega e si deforma sotto il suo peso; possiamo dire che la carica ha modificato lo stato di tensione dello spazio.

Prendiamo, ora, una seconda carica q, molto più piccola della precedente, detta carica esploratrice, in quanto il modo in cui essa modifica lo spazio è trascurabile rispetto all’altra.

Se poniamo la carica q all’interno dello spazio che era già stato modificato da Q, essa risente di tale deformazione, e viene attratta verso la carica generatrice.

Possiamo immaginare questo fatto osservando cosa accade se poniamo una sfera di piccole dimensioni ai lati del telo deformato: la pallina tende a scivolare nella direzione della massa più grande.

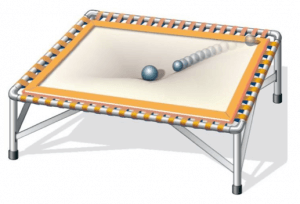
La carica di prova q è attratta dalla carica generatrice Q perché sottoposta alla forza di Coulomb.

Definizione del vettore campo elettrico

Ricordiamo che la forza che lega le due cariche è una grandezza vettoriale, ed è data dalla seguente espressione:

$vec F = k_0 * frac(Q*q)(r^2) * vec u$

Dove il vettore $ vec u$ è un vettore unitario, che giace sulla retta congiungente le due cariche, e verso che dipende dal segno di esse.

Come detto in precedenza, dalle supposizioni di Faraday il campo elettrico sussiste anche in assenza della seconda carica, quella di prova; di conseguenza, possiamo definire il vettore campo elettrico in questo modo:

$vec E = frac(vec F)(q) = k_0 * frac(Q)(r^2) * vec u $

Il vettore campo elettrico ha stessa direzione del vettore forza; il suo verso, invece, dipende dal segno della carica di prova: se la carica q ha segno positivo, allora il vettore campo elettrico e il vettore forza hanno lo stesso verso, altrimenti hanno verso opposto.

Come sappiamo, all’interno di un mezzo, come l’acqua per esempio, il valore della forza elettrica è minore di quello che si avrebbe nel vuoto, in quanto le particelle del mezzo tendono a schermare la carica in questione.

Anche il modulo del campo elettrico, quindi, varia, e rispetto a quello nel vuoto risulta diviso per un fattore 4πε:

$ E_m = frac(F_m)(q) =frac(k_0)(ε_r) * frac(Q)(r^2) $